斐波那契(fibonacci)
斐波那契数列(Fibonacci sequence),又称黄金分割数列、因数学家列昂纳多·斐波那契(Leonardoda Fibonacci)以兔子繁殖为例子而引入,故又称为“兔子数列”,指的是这样一个数列:1、1、2、3、5、8、13、21、34、……在数学上,斐波纳契数列以如下被以递归的方法定义:F(0)=0,F(1)=1, F(n)=F(n-1)+F(n-2)(n>=2,n∈N*)在现代物理、准晶体结构、化学等领域,斐波纳契数列都有直接的应用,为此,美国数学会从1963起出版了以《斐波纳契数列季刊》为名的一份数学杂志,用于专门刊载这方面的研究成果。
斐波那契(fibonacci)应用
蒙拉丽莎的微笑
斐波那契(fibonacci)数列代码实例
假设兔子在2个月之后就有了繁殖能力,每个月可以产下一对兔子,如果不考虑死亡的售后,一年后他们总共有多少对兔子。
迭代
- def tuzidd(n):
- n1 = 1 #第一个月是1
- n2 = 1 #第二个月还是1
- n3 = 1 #第三个月默认是一
- if n < 1:
- print('输入有误')
- return -1
- while (n-2)>0:
- n3 = n2 + n1
- print(n3,n2,n1)
- #2 1 1
- #3 2 1
- #5 3 2
- #5
- n1 = n2
- n2 = n3
- n -= 1
- return n3
- print(tuzidd(5))
其实一开始是不理解的,后面在代码中布置了print,来判断每一次的结果,后面就看得比较明显了。右边赋值给左边
递归
- # 递归计算20个月的兔子数量
- def tuzi(n):
- if n==1 or n ==2:
- return 1
- elif n >2:
- return tuzi(n -2) + tuzi(n -1)
- print(tuzi(12))
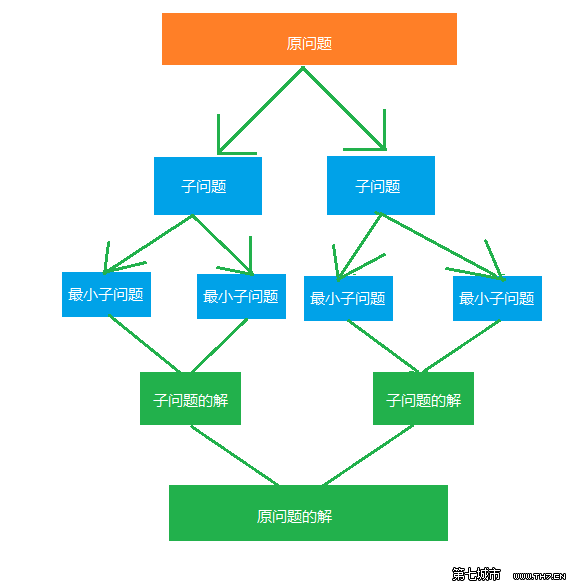
分治算法
分治算法的基本思想是将一个规模为N的问题分解为K个规模较小的子问题,这些子问题相互独立且与原问题性质相同。求出子问题的解,就可得到原问题的解。即一种分目标完成程序算法,简单问题可用二分法完成。
单词扩展:
- fibonacci:斐波那契
扩展阅读:
版权注释:
Python课程来源于鱼C论坛:http://bbs.fishc.com/forum-243-1.html 版块,课程内容为免费内容,如果你喜欢该课程,建议购买VIP账号支持小甲鱼,官方网店:https://fishc.taobao.com/)。
本内容为在李金龙在学习课程中做的日记记录,方便自己以后查找相关信息,另一方面也希望自己写下的东西可以帮助到别人。
课程内容:http://blog.fishc.com/3132.html